Lab 6 [GIS5935]: Scale Effect and Spatial Data Aggregation

In this lab, we examined the effects of scale and resolution on the properties of spatial data. On vector data, as scale becomes finer, we expect to see increases in the number of areas and volumes, more detail in boundaries, and more homogeneity in the features (Goodchild, 2011, pp. 6). This occurs because coarser scales (e.g., 1:100000) are more generalized, and thus a smaller number of polygons capture the most significantly sized features, while omitting smaller features. As more details are captured at finer scales (e.g., 1:1200) compared to coarser scales, geometric characteristics such as the sum of total lengths for hydrographic features will increase, based on the addition of the captured smaller features.

On raster data, as resolution becomes coarser (e.g., going from 1x1m to 90x90m cells), the image becomes more smoothed, as represented by increasingly smaller average slopes as steep regions are averaged into surrounding non-steep terrain regions. Kienzle observed this when studying geomorphological features at cell sizes of 50, 100, and 250 m and noted mean slope values decreased as the grid cell size increased (Kienzle, 2004, pp. 86). In addition, it was observed in this work that greater cell sizes caused greater underestimations of slope (Kienzle, 2004, pp. 94). The larger impacts of this for professional practice are that we should pay particular attention to scale when using slope values to determine stability or erosion if the DEM is at a coarse resolution, because the slope values are likely higher than estimates at this scale indicate, particularly at resolutions greater than 2.5 m (Kienzle, 2004, pp. 94).

In the second part of the lab we studied spatial analyses related to gerrymandering, which is the practice of manipulating the boundaries of polygons associated with districts for unfair political advantage (Wikipedia, n.d.). Gerrymandering can be measured with geoprocessing tools designed to mathematically capture a metric describing the fairness of the polygon boundary capturing the district. One such metric is the Polsby-Popper test for compactness, measured as:

(4.0*math.pi * !Shape_Area!) / (!Shape_Length! * !Shape_Length!)

With this equation, the closer a Polsby-Popper value is to 1, the more compact (and thus fair) the polygon is. Here is a screenshot of an 'offending' district which fails to have district 'compactness' as measured by a Polsby-Popper value of 0.09: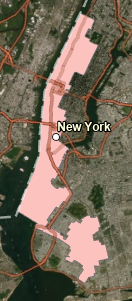


Comments

Post a Comment

Popular posts from this blog

Lab 2 [GIS5935]: Data Quality Standards

Image
  The image above shows 20 test point locations across a street map for the city of Albuquerque. In selecting these test points to report the horizontal accuracy of two alternative geographic data sources providing street centerlines, the following constraints were applied, in compliance with using the National Standard for Spatial Data Accuracy to measure and report the associated quality (Minnesota Planning Land Management Information Center, 2019): Locations were selected using street intersections derived from orthophotos of the study area - these images contained detailed imagery of street centerlines and nearby features (e.g., medians, sidewalks) that could be readily used to accurately determine intersection points. Given the street uniformity throughout the region, approximately 25% of the points were derived from each quadrant of the overall study area, and all quadrants were equally represented in this way (meeting the requirement to draw at least 20% of test points from each
Read more

Lab 5 [GIS5935]: Surface Interpolation

Image
  In this lab we examined various interpolation methods to create a surface of water quality in Tampa Bay. Each method received as input a set of sample points containing Biochemical Oxygen Demand (BOD) values in milligrams per liter that were recorded from various points throughout the study region. The interpolation methods used this case study included the following: Thiessen IDW Spline - Regularized Spline - Tension This interpolation method is a special case of IDW where only the nearest water sample is used to estimate the BOD value at an unsampled location. This interpolation method uses a preset number of nearest neighbors to estimate the BOD value at an unsampled location, and inversely weights the contributing strength of these neighbors based on their distances from the unsampled location. Spline interpolation methods work to fit a smooth surface exactly touching the BOD sampled points, while
Read more

Final Project [GIS6005]: Conservation in the State of Florida: Preserving Key Habitats of the Striped Burrfish

Image
Striped burrfish are inshore fish known to exploit a wide range of depths. Although commonly found in grass beds around barrier islands in the Gulf of Mexico (Franks et al., 1972), they are also found near coral reefs (Robins, Ray, & Douglas, 1986), as well as in deeper waters during the winter months (Audubon Society, 2002). Changes to the geographic ranges of fish species due to factors such as ocean warming (Espino et al., 2019) are of concern to scientists. In addition, impacts to fish habitats in tourism-based states such as Florida are considered by economists given the socioeconomic benefits of commercial and recreational fishing to coastal communities (Lellis-Dibble, McGlynn, & Bigford, 2008). As one example of their impact, half of all federally managed fisheries in the U.S. depend on coral reefs (Burton, 2019). In addition, t he total value of coral reefs for southeast Florida was estimated in 2007 to be $174 million/year (Brander & van Beukering, 2013),
Read more